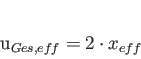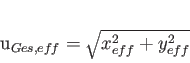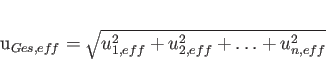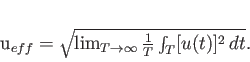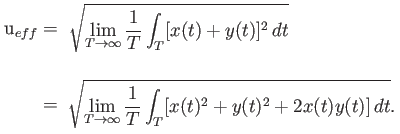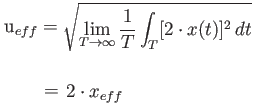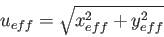Bis jetzt wurde noch nicht behandelt, wie hoch der Pegel eines Signals u(t)=x(t)+y(t) ist, das die Summe zweier Signale darstellt. Wie in Abschnitt ??? ausgeführt, steht im Argument des Logarithmus ein Effektivwert. Leider lassen sich Effektivwerte resp. Leistungen nicht so einfach addieren, wie man das vielleicht erwarten könnte. Es zeigt sich nämlich, daß es bei der Addition eine Rolle spielt, ob sich die Signale, welche addiert werden, ähnlich sind oder nicht.
Zur Erläuterung müssen erst einige Begriffe eingeführt werden, die leider anschaulich schwer zu fassen sind.
[8]Zwei Signale heißen kohärent, wenn ein Signal nur gegen sich selber verschoben und skaliert wurde, beispielsweise wenn sie von der gleichen Quelle kommen. Laufzeit- bzw. Pegelunterschiede spielen also keine Rolle.
Zwei Signale heißen hingegen inkohärent, wenn sie einander zu keinem Zeitpunkt in irgendeiner Weise ähnlich sind.
Die Korrelation gibt die Verwandtschaft zweier Signale zu einem bestimmten Zeitpunkt pegelunabhängig an. Signale sind also korreliert, wenn sie bis auf einen Skalierungsfaktor übereinstimmen. Der sogenannte Korrelationsgrad zeigt die Ähnlichkeit auf einer Skala zwischen [-1;1] an; dabei steht «1» für Gleichheit, «-1» für Gegenphasigkeit und «0» für Unkorreliertheit.
Dies bedeutet einerseits, daß inkohärente Signale immer unkorreliert sind, andererseits korrelierte Signale immer kohärent sind. Umgekehrt trifft dies nicht allgemein zu.
Beispiel 3.1.
Rauschen ist zu allen Signalen (außer zu sich selbst) inkohärent und damit auch unkorreliert.
Eine Sinus- und eine Cosinusschwingung sind zwar unkorreliert zueinander, aber kohärent.
Die Ausgangssignale zweier Mikrophone sind (wenn die Mikrophone nicht zu nah beieinander stehen) näherungsweise unkorreliert.
Hinweis
In der Technik und Mathematik wird oft der Begriff orthogonal statt nicht korreliert verwendet. Die Bedingung für Unkorreliertheit bzw. Orthogonalität zweier Signale x(t),y(t) ist ∫x(t) · y(t)dt=0
Man stelle sich nun die zu addierenden Signale als Vektoren vor (siehe Abbildung 3.2, „ Veranschaulichung der Addition von Effektivwerten “), deren Betrag ihr Effektivwert ist. Sind zwei Signale identisch, so haben die zugehörigen Vektoren den gleichen Betrag und die gleiche Orientierung. Sind sie hingegen unkorreliert, so stehen die Vektoren senkrecht aufeinander (90° Phasenverschiebung!). Das gewünschte Ergebnis, nämlich der Effektivwert des resultierenden Signals, ist der Betrag des aus der Addition resultierenden Vektors.
Für die Addition zweier gleicher Signale x erhält man also
Der Pegel des resultierenden Signals nimmt also um 20 · log(2) = 6 [dB] zu.
Bei der Addition zweier nicht korrelierter Signale x und y erhalten wir
Für xeff=yeff erhält man hier eine Zunahme um
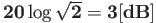 ! Bei der Addition von unkorrelierten
Signalen gleichen Pegels nimmt der Pegel
also um 3 dB zu.
! Bei der Addition von unkorrelierten
Signalen gleichen Pegels nimmt der Pegel
also um 3 dB zu.
Beispiel 3.2.
Das Rauschen zweier Tonbandspuren, die mit gleichem Pegel gemischt werden, ist um 3dB lauter als das einer Spur.
Werden nun mehrere nicht korrelierte Quellen gleichen Pegels addiert, so erhält man analog dazu:
und der Gesamtpegel nimmt dementsprechend um 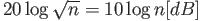 zu.
zu.
Haben die Quellen nicht denselben Pegel, so muß man in die obigen Gleichungen die entsprechenden Effektivwerte einsetzen und hat etwas mehr Arbeit. Die Rechnung ist aber im Prinzip identisch.
Hinweis
Es gibt natürlich beliebige Zwischenstufen zwischen unkorreliert und identisch (siehe ???). In einem solchen Fall stehen die Vektoren dann nicht mehr senkrecht aufeinander und der resultierende Pegel wird bei der Addition von zwei Signalen zwischen 3 und 6dB liegen.
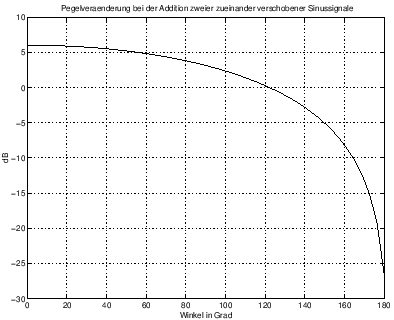
Abbildung 3.3. Pegeländerung bei der Addition zweier zueinander verschobener Sinussignale. Für einen Phasenwinkel von 0° ergeben sich 6dB Pegelzunahme, während der Pegel des resultierenden Signals für einen Winkel von 180° gegen $-\infty$ geht
Für die Leser, die es etwas genauer wissen wollen, folgt eine etwas detailliertere Herleitung:
Um die erhaltenen Resultate zu überprüfen, muß die Definition des Effektivwertes betrachtet werden, die ja lautete
Dementsprechend gilt also für den Effektivwert, wenn u(t) die Summe zweier Signale x(t) und y(t) ist
Für den Fall, daß x(t)=y(t) ist, erhält man
also das Ergebnis, das nach Gleichung Gleichung 3.8 schon erwartet werden konnte.
Sind x und y nicht korreliert, so gilt für die Gleichung Gleichung 3.12, daß das Integral über den gemischten Term gleich 0 ist (dies gilt aufgrund der Orthogonalitätseigenschaft, die als mathematische Definition der Unkorreliertheit gegeben wurde). Mit Hilfe der Orthogonalitätseigenschaft unkorrelierter Signale folgt also
und damit Gleichung Gleichung 3.9.
Bisher ging es um die elektrische Addition von Signalen. Sollen diese akustisch addiert werden, so ergeben sich andere Pegelunterschiede. Im allgemeinen sind Schallwellen im Raum bei zwei Sendern nicht mehr korreliert, auch wenn die Sender selbst das gleiche Signal abstrahlen. Dementsprechend erhöht sich der Schalldruckpegel bei zwei Lautsprechern, welche das gleiche Signal abstrahlen, um 3dB.
Beispiel 3.3.
Zwei Lautsprecher, die mit dem gleichen Signal gespeist werden, erzeugen einen Schalldruckpegel, der um 3dB höher ist als der von einem einzigen Lautsprecher erzeugte Pegel.
Zwei gleiche und gleichlaute Musikinstrumente spielen unisono 3dB lauter als ein einzelnes.
[8] Es kann sein, daß diese Begriffe an anderer Stelle anders eingeführt werden. Es wurde versucht, die Definition der beiden Begriffe Inkohärenz und Korrelation möglichst aus dem gängigen Gebrauch in der Aufnahmepraxis herzuleiten. Aus diesem Grund muß man sich bei der Lektüre verschiedener Literatur immer vergewissern, in welchem Sinn die Begriffe Kohärenz und Korrelation benutzt werden.